mirror of https://github.com/inclusionAI/AReaL
197 lines
5.2 KiB
Markdown
197 lines
5.2 KiB
Markdown
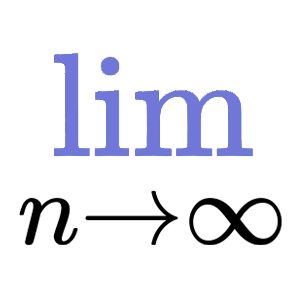
|
||
|
||
# [latex2sympy2](https://github.com/OrangeX4/latex2sympy)
|
||
|
||
## About
|
||
|
||
`latex2sympy2` parses **LaTeX math expressions** and converts it into the equivalent **SymPy form**. The latex2sympy2 is adapted from [augustt198/latex2sympy](https://github.com/augustt198/latex2sympy) and [purdue-tlt / latex2sympy](https://github.com/purdue-tlt/latex2sympy).
|
||
|
||
This project is a part of a VS Code extension called [Latex Sympy Calculator](https://marketplace.visualstudio.com/items?itemName=OrangeX4.latex-sympy-calculator). It is designed for providing people writing in latex or markdown a ability to calculate something when writing math expression.
|
||
|
||
[ANTLR](http://www.antlr.org/) is used to generate the parser.
|
||
|
||
## Features
|
||
|
||
* **Arithmetic:** Add (+), Sub (-), Dot Mul (·), Cross Mul (×), Frac (/), Power (^), Abs (|x|), Sqrt (√), etc...
|
||
* **Alphabet:** a - z, A - Z, α - ω, Subscript (x_1), Accent Bar(ā), etc...
|
||
* **Common Functions:** gcd, lcm, floor, ceil, max, min, log, ln, exp, sin, cos, tan, csc, sec, cot, arcsin, sinh, arsinh, etc...
|
||
* **Funcion Symbol:** f(x), f(x-1,), g(x,y), etc...
|
||
* **Calculous:** Limit ($lim_{n\to\infty}$), Derivation ($\frac{d}{dx}(x^2+x)$), Integration ($\int xdx$), etc...
|
||
* **Linear Algebra:** Matrix, Determinant, Transpose, Inverse, Elementary Transformation, etc...
|
||
* **Other:** Binomial...
|
||
|
||
**NOTICE:** It will do some irreversible calculations when converting determinants, transposed matrixes and elementary transformations...
|
||
|
||
## Installation
|
||
|
||
```
|
||
pip install latex2sympy2
|
||
```
|
||
|
||
**Requirements:** `sympy` and `antlr4-python3-runtime` packages.
|
||
|
||
## Usage
|
||
|
||
### Basic
|
||
|
||
In Python:
|
||
|
||
```python
|
||
from latex2sympy2 import latex2sympy, latex2latex
|
||
|
||
tex = r"\frac{d}{dx}(x^{2}+x)"
|
||
# Or you can use '\mathrm{d}' to replace 'd'
|
||
latex2sympy(tex)
|
||
# => "Derivative(x**2 + x, x)"
|
||
latex2latex(tex)
|
||
# => "2 x + 1"
|
||
```
|
||
|
||
### Examples
|
||
|
||
|LaTeX|Converted SymPy|Calculated Latex|
|
||
|-----|-----|---------------|
|
||
|`x^{3}` $x^{3}$| `x**3`|`x^{3}` $x^{3}$|
|
||
|`\frac{d}{dx} tx` $\frac{d}{dx}tx$|`Derivative(x*t, x)`|`t` $t$|
|
||
|`\sum_{i = 1}^{n} i` $\sum_{i = 1}^{n} i$|`Sum(i, (i, 1, n))`|`\frac{n \left(n + 1\right)}{2}` $\frac{n \left(n + 1\right)}{2}$|
|
||
|`\int_{a}^{b} \frac{dt}{t}`|`Integral(1/t, (t, a, b))`|`-\log{(a)} + \log{(b)}` $-\log{(a)} + \log{(b)}$|
|
||
|`(2x^3 - x + z)|_{x=3}` $(2x^3 - x + z)\|_{x=3}$|`z + 51`| `z + 51` $z + 51$ |
|
||
|
||
If you want to read the math formula, you can click [GitNotes](https://notes.orangex4.cool/?git=github&github=OrangeX4/latex2sympy).
|
||
|
||
### Solve Equation
|
||
|
||
``` latex
|
||
# Before
|
||
x + y = 1
|
||
|
||
# After
|
||
[ y = 1 - x, \ x = 1 - y]
|
||
```
|
||
|
||
### Eval At
|
||
|
||
``` latex
|
||
# Before
|
||
(x+2)|_{x=y+1}
|
||
|
||
# After
|
||
y + 3
|
||
```
|
||
|
||
### Matrix
|
||
|
||
#### Identity matrix
|
||
|
||
```
|
||
tex = r"\bm{I}_3"
|
||
latex2sympy(tex)
|
||
# => "Matrix([[1, 0, 0], [0, 1, 0], [0, 0, 1]])"
|
||
```
|
||
|
||
#### Determinant
|
||
|
||
``` python
|
||
from latex2sympy2 import latex2sympy
|
||
|
||
tex = r"\begin{vmatrix} x & 0 & 0 \\ 0 & x & 0 \\ 0 & 0 & x \end{vmatrix}"
|
||
latex2sympy(tex)
|
||
# => "x^{3}"
|
||
```
|
||
|
||
#### Transpose
|
||
|
||
``` python
|
||
from latex2sympy2 import latex2sympy
|
||
|
||
tex = r"\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}^T"
|
||
# Or you can use "\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}'"
|
||
latex2sympy(tex)
|
||
# => "Matrix([[1, 4, 7], [2, 5, 8], [3, 6, 9]])"
|
||
```
|
||
|
||
#### Elementary Transformation
|
||
|
||
``` python
|
||
from latex2sympy2 import latex2sympy
|
||
|
||
matrix = r'''
|
||
\begin{pmatrix}
|
||
1 & 2 & 3 \\
|
||
4 & 5 & 6 \\
|
||
7 & 8 & 9 \\
|
||
\end{pmatrix}
|
||
'''
|
||
|
||
# Scale the row with grammar "\xrightarrow{kr_n}"
|
||
tex = matrix + r'\xrightarrow{3r_1}'
|
||
latex2sympy(tex)
|
||
# => "Matrix([[3, 6, 9], [4, 5, 6], [7, 8, 9]])"
|
||
|
||
# Swap the cols with grammar "\xrightarrow{c_1<=>c_2}"
|
||
# Of course, you can use "\leftrightarrow" to replace "<=>"
|
||
tex = matrix + r'\xrightarrow{c_1<=>c_2}'
|
||
latex2sympy(tex)
|
||
# => "Matrix([[2, 1, 3], [5, 4, 6], [8, 7, 9]])"
|
||
|
||
# Scale the second row and add it to the first row
|
||
# with grammar "\xrightarrow{r_1+kr_2}"
|
||
tex = matrix + r'\xrightarrow{r_1+kr_2}'
|
||
latex2sympy(tex)
|
||
# => "Matrix([[4*k + 1, 5*k + 2, 6*k + 3], [4, 5, 6], [7, 8, 9]])"
|
||
|
||
# You can compose the transform with comma ","
|
||
# and grammar "\xrightarrow[4r_3]{2r_1, 3r_2}"
|
||
# Remember the priority of "{}" is higher than "[]"
|
||
tex = matrix + r'\xrightarrow[4r_3]{2r_1, 3r_2}'
|
||
latex2sympy(tex)
|
||
# => "Matrix([[2, 4, 6], [12, 15, 18], [28, 32, 36]])"
|
||
```
|
||
|
||
### Variances
|
||
|
||
``` python
|
||
from latex2sympy2 import latex2sympy, variances, var, set_variances
|
||
|
||
# Assign x a value of 1
|
||
latex2sympy(r"x = 1")
|
||
|
||
# Assign x a matrix symbol with dimension of n x m
|
||
latex2sympy(r"x \in \mathbb{R}^{n \times m}")
|
||
|
||
# Calculate x + y
|
||
latex2sympy(r"x + y")
|
||
# => "y + 1"
|
||
|
||
# Get all variances
|
||
print(variances)
|
||
# => "{x: 1}"
|
||
|
||
# Get variance of "x"
|
||
print(var["x"])
|
||
# => "1"
|
||
|
||
# Reset all variances
|
||
set_variances({})
|
||
latex2sympy(r"x + y")
|
||
# => "x + y"
|
||
```
|
||
|
||
### Complex Number Support
|
||
|
||
``` python
|
||
from latex2sympy2 import set_real
|
||
|
||
set_real(False)
|
||
```
|
||
|
||
|
||
## Contributing
|
||
|
||
If you want to add a new grammar, you can fork the code from [OrangeX4/latex2sympy](https://github.com/OrangeX4/latex2sympy).
|
||
|
||
* To modify parser grammar, view the existing structure in `PS.g4`.
|
||
* To modify the action associated with each grammar, look into `latex2sympy.py`.
|
||
|
||
Contributors are welcome! Feel free to open a pull request or an issue.
|